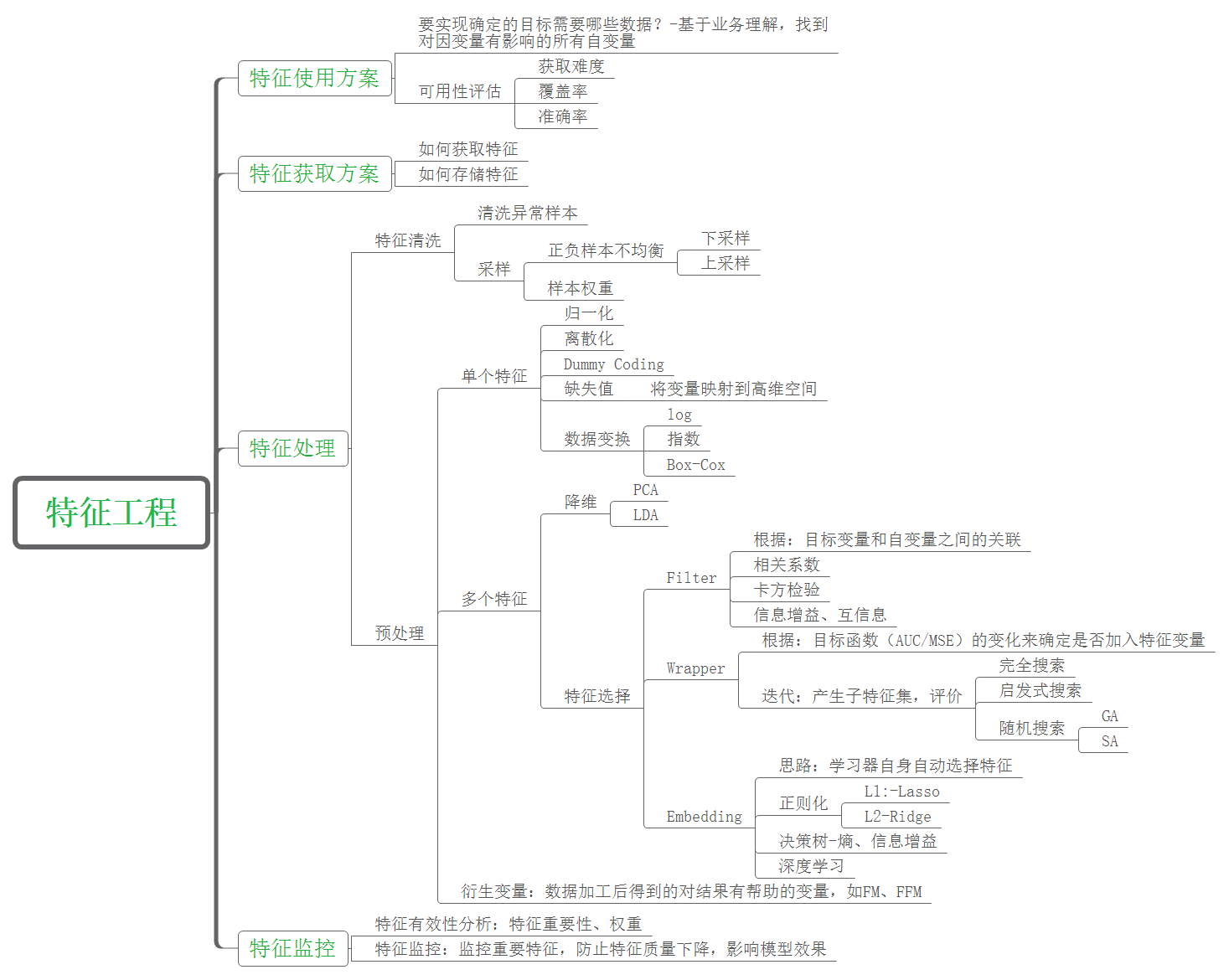
概述
- 机器学习将数据拟合到数学模型中来获得结论或者做出预测。这些模型吸纳特征作为输入。特征就是原始数据某方面的数学表现。在机器学习流水线中特征位于数据和模型之间。
- 特征工程是一项从数据中提取特征,然后转换成适合机器学习模型的格式的艺术。这是机器学习流水线关键的一步,因为正确的特征可以减轻建模的难度,并因此使流水线能输出更高质量的结果。
- 数据和特征决定了机器学习的上限, 而模型和算法只是逼近这个上限而已.
- 流程:

分类
数据清洗
数据样本采集(抽样)
- 样本要具有代表性
- 样本比例要平衡以及样本不平衡时如何处理
- 考虑全量数据
缺失值
- 缺失值的比例超过50%以上时, 此字段通常舍弃不用, 不做任何填补.
- 另一种处理, 将此字段的值根据是否缺失, 生成指示变量, 将原字段舍弃, 并仅使用此指示变量作为输入变量.
异常值(空值)处理
- 识别异常值和重复值
- Pandas: isnull()/duplicated()
- 直接丢弃(包括重复值)
- Pandas: drop()/dropna()/drop_duplicated()
- 当是否有异常当做一个新的属性, 替代原值
- 集中值指代: 除异常值以外的均值, 中位数, 众数等
- 边界值指代: 连续值中使用四分位间距确定的上下边界来确定超过上下边界的数
- 插值
- Pandas: interpolate()–Series
特征预处理
- 分类
- 特征选择
- 特征变换
- 对数化, 离散化, 数据平滑, 归一化(标准化), 数值化, 正规化
- 特征降维
- 特征衍生
特征选择
特征变换
对指化
离散化
- 概述:
- 方法:
- 优点:
- 可使数据精简, 降低数据的复杂度, 让数据更容易被解释.
- 可支持许多无法处理数值型属性的分类算法, 如贝叶斯分类算法, 以关联规则为基础的分类算法.
- 可提高分类器的稳定性, 进而提升分类模型的准确度.
- 可找出条件属性在目标属性上的趋势(Trend), 有助于未来的解读.
无量纲化
- 分类: 区间缩放, 标准化和归一化
- 使用时机
1、在后续的分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA、LDA这些需要用到协方差分析进行降维的时候,同时数据分布可以近似为正太分布,标准化方法(Z-score standardization)表现更好.
2. 在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用区间缩放法或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围.
区间缩放(对列向量处理)
- Min-Max
- 数据缩放到(0,1)之间
$$x’ = \frac{x - x_{\min}}{x_{\max} - x_{\min}}$$
- 示例
import numpy as np
from sklearn.preprocessing import MinMaxScaler
# 归一化
MinMaxScaler().fit_transform(np.array([1,4,10,15,21]).reshape(-1,1))
# array([[0. ],
# [0.15],
# [0.45],
# [0.7 ],
# [1. ]])
MinMaxScaler().inverse_transform(result) # 将归一化后的结果逆转
# 当X中特征太多时, 使用partial_fit作为训练接口
标准化(对列向量处理)
- 标准化的前提是特征值服从正态分布,标准化后,其转换成标准正态分布。
- Z-score
$$x’= \frac{x - \bar{x}}{\sigma}$$
- 示例
import numpy as np
from sklearn.preprocessing import StandardScaler
# 标注化
StandardScaler().fit_transform(np.array([1,1,1,1,0,0,0,0]).reshape(-1,1))
# array([[ 1.],
# [ 1.],
# [ 1.],
# [ 1.],
# [-1.],
# [-1.],
# [-1.],
# [-1.]])
归一化(对行向量处理)
- 归一化目的在于样本向量在点乘运算或其他核函数计算相似性时,拥有统一的标准,也就是说都转化为“单位向量”.
- 公式
$$x’= \frac{x_{i}}{\sqrt{\sum_{j=1}^{n} |x_{j}|^{2}}}$$
- 示例
from sklearn.datasets import load_iris
#导入IRIS数据集
iris = load_iris()
#特征矩阵
iris.data
#目标向量
iris.target
from sklearn.preprocessing import Normalizer
#归一化,返回值为归一化后的数据
Normalizer().fit_transform(iris.data)
数值化
- 数据分类:
- 定类: 数值化-独热(One-Hot Encode)
- 定序: 数值化-标签化
- 定距: 归一化
- 定比
- 示例
# 使用pandas
import pandas as pd
# onehot_cols 为需要进行哑变量的数组列
pd.get_dummies(whole_df[onehot_cols], dummy_na = True)
# 使用sklearn
from sklearn.preprocessing import LabelEncoder,OneHotEncoder
LabelEncoder().fit_transform(np.array(["Down", "Up", "Up", "Down"]).reshape(-1,1))
# array([0, 1, 1, 0])
lb_encoder = LabelEncoder()
lb_tran = lb_encoder.fit_transform(np.array(["Red", "Yellow", "Blue", "Green"]))
oht_encoder = OneHotEncoder().fit(lb_tran.reshape(-1,1))
oht_encoder.transform(lb_encoder.transform(np.array(["Yellow", "Blue", "Green", "Green", "Red"])).reshape(-1,1))
oht_encoder.transform(lb_encoder.transform(np.array(["Yellow", "Blue", "Green", "Green", "Red"])).reshape(-1,1)).toarray()
# array([[0., 0., 0., 1.],
# [1., 0., 0., 0.],
# [0., 1., 0., 0.],
# [0., 1., 0., 0.],
# [0., 0., 1., 0.]])
one-hot encoding与dummy encoding
- one-hot encoding: 将离散型特征的每一种取值都看成一种状态,若你的这一特征中有N个不相同的取值,那么我们就可以将该特征抽象成N种不同的状态,one-hot编码保证了每一个取值只会使得一种状态处于“激活态”,也就是说这N种状态中只有一个状态位值为1,其他状态位都是0。
- dummy encoding: 任意的将一个状态位去除。
- 最好是选择正则化 + one-hot编码;哑变量编码也可以使用,不过最好选择前者。虽然哑变量可以去除one-hot编码的冗余信息,但是因为每个离散型特征各个取值的地位都是对等的,随意取舍未免来的太随意。
正规化(规范化)
- 常用
- L1距离:
$$x’= \frac{x_i}{\sum_{j=1}^n|x_j|}$$
- L2距离:
$$x’= \frac{x_i}{\sqrt{\sum_{j=1}^n|x_j|^2}}$$
- 场景:
- 直接用在特征上(比较少)
- 用在每个对象的各个特征的表示(特征矩阵的行)
- 模型的参数上(回归模型使用较多)
- 示例
from sklearn.preprocessing import Normalizer
# L1距离
Normalizer(norm='l1').fit_transform(np.array([1,1,3,-1,2]).reshape(-1,1))
# array([[ 1.],
# [ 1.],
# [ 1.],
# [-1.],
# [ 1.]])
# L2距离
Normalizer(norm='l2').fit_transform(np.array([[1,1,3,-1,2]]))
# array([[ 0.25, 0.25, 0.75, -0.25, 0.5 ]])
连续变量压缩
特征降维
PCA, 奇异值分解等线性降维
- PCA:
- 求特征协方差矩阵
- 求协方差的特征值和特征向量
- 将特征值按照大小排序, 选择其中最大的k个
- 将样本点投影到选取的特征向量上
LDA降维
- 概述
- 线性判别式分析(Liner Discriminant Analysis)
- 核心思想:
- 投影变化后同一标注内距离尽可能小
- 不同标注间距离尽可能大
分类变量压缩技术
特征衍生
参考