机器学习中的评估指标

发表于： 2019-09-08 更新于： 2024-04-04 分类于：数据科学

字数： 848 阅读：≈ 4分钟浏览：评论：

分类问题

当正负样本分布极不均衡时, 准确率将失去意义, 通常使用AUC作为指标

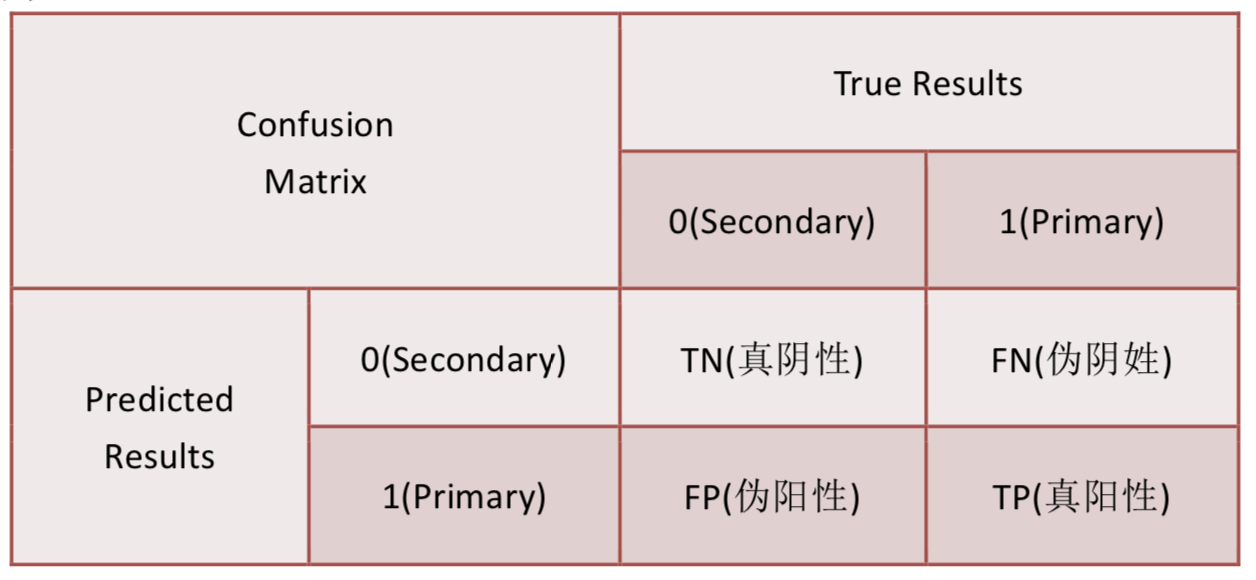
混淆矩阵（Confusion Matrix）

矩阵中的每一行代表实例的预测类别，每一列代表实例的真实类别。

真正(True Positive , TP)：被模型预测为正的正样本。
假正(False Positive , FP)：被模型预测为正的负样本。
假负(False Negative , FN)：被模型预测为负的正样本。
真负(True Negative , TN)：被模型预测为负的负样本。

真正率(True Positive Rate,TPR)：TPR=TP/(TP+FN)，即被预测为正的正样本数 /正样本实际数。 召回率
假正率(False Positive Rate,FPR) ：FPR=FP/(FP+TN)，即被预测为正的负样本数 /负样本实际数。
假负率(False Negative Rate,FNR) ：FNR=FN/(TP+FN)，即被预测为负的正样本数 /正样本实际数。
真负率(True Negative Rate,TNR)：TNR=TN/(TN+FP)，即被预测为负的负样本数 /负样本实际数/2

sklearn相应的包

sklearn.metrics.confusion_matrix

from sklearn.metrics import confusion_matrix
# y_pred是预测标签
y_pred, y_true =[1,0,1,0], [0,0,1,0]
confusion_matrix(y_true=y_true, y_pred=y_pred)
# array([[2, 1],
#        [0, 1]], dtype=int64)

准确率(Accuracy)

分类正确的样本个数占总样本的比例.

sklearn相应的包

sklearn.metrics.accuracy_score

from sklearn.metrics import accuracy_score
# y_pred是预测标签
y_pred, y_true=[1,2,3,4], [2,2,3,4]
accuracy_score(y_true=y_true, y_pred=y_pred)
# 0.75

精确率(Precision): 预测正确的正样本占所有预测为正样本的比例

所有分正确的正样本/所有预测为正类的样本数. $$Precision = \frac{TP}{TP + FP}$$
也叫查准率

sklearn相应的包

sklearn.metrics.precision_score

from sklearn.metrics import precision_score
# y_pred是预测标签
y_pred, y_true =[1,0,1,0], [0,0,1,0]
precision_score(y_true=y_true, y_pred=y_pred)
# 0.5

召回率 (Recall): 预测正确的正样本占所有正样本比例

所有分正确的正样本/所有的正样本数. $$Recall = \frac{TP}{TP + FN}$$
也叫查全率

sklearn

sklearn.metrics.recall_score

from sklearn.metrics import recall_score
# y_pred是预测标签
y_pred, y_true =[1,0,1,0], [0,0,1,0]
recall_score(y_true=y_true, y_pred=y_pred)
# 1.0

F1 score

又称平衡分数, 定义为精确率和召回率的调和平均数 $$F_1 \ score = \frac{2 * Precision * Recall}{Precision + Recall}$$

sklearn相应的包

sklearn.metrics.f1_score

from sklearn.metrics import f1_score
# y_pred是预测标签
y_pred, y_true =[1,0,1,0], [0,0,1,0]
f1_score(y_true=y_true, y_pred=y_pred)

# classification_report可以直接输出各个类的precision recall f1-score support
from sklearn.metrics import classification_report
# y_pred是预测标签
y_pred, y_true =[1,0,1,0], [0,0,1,0]
print(classification_report(y_true=y_true, y_pred=y_pred))

增益（Gain）和提升（Lift）图

ROC曲线

横轴: 负正类率(false postive rate FPR=FP/(FP+TN))特异度, 划分实例中所有负例占所有负例的比例；(1-Specificity)
纵轴: 真正类率(true postive rate TPR=TP/(TP+FN))灵敏度, Sensitivity(正类覆盖率), 即召回率

sklearn相应的包

sklearn.metrics.roc_curve, sklearn.metrics.auc

import matplotlib.pyplot as plt 
from sklearn.metrics import roc_curve, auc
# y_test：实际的标签, dataset_pred：预测的概率值。
fpr, tpr, thresholds = roc_curve(y_test, dataset_pred)
roc_auc = auc(fpr, tpr)  
#画图，只需要plt.plot(fpr,tpr),变量roc_auc只是记录auc的值，通过auc()函数能计算出来  
plt.plot(fpr, tpr, lw=1, label='ROC(area = %0.2f)' % (roc_auc))
plt.xlabel("FPR (False Positive Rate)")
plt.ylabel("TPR (True Positive Rate)")
plt.title("Receiver Operating Characteristic, ROC(AUC = %0.2f)"% (roc_auc))
plt.show()

AUC（Area Under Curve）

AUC即为ROC曲线下的面积(ROC的积分), 通常大于0.5小于1.
AUC值(面积)越大的分类器，性能越好.

sklearn相应的包

sklearn.metrics.roc_auc_score

from sklearn.metrics import roc_auc_score
# y_test：实际的标签, dataset_pred：预测的概率值。
roc_auc_score(y_test, dataset_pred)

PR曲线

横坐标: 精确率P
纵坐标: 召回率R
评价标准和ROC一样，先看平滑不平滑（蓝线明显好些）。一般来说，在同一测试集，位于上面的线比下面的好.
当P和R的值接近时，F1值最大.

曲线绘制

import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from sklearn.metrics import precision_recall_fscore_support as prfs


def evaluate_pr(res, inf=0.0, sup=1.0):
    y_vali = res.copy()
    pres = []
    recs = []
    thrs = []
    for thred in np.arange(inf, sup, 0.01):
        y_vali['pred'] = y_vali['proba'] > thred
        p, r, f, _ = prfs(y_vali['real'], y_vali['pred'], average='binary')
        pres.append(p)
        recs.append(r)
        thrs.append(thred)
    sns.lineplot(pres, recs)

proba = model.predict_proba(X)[:,1]
res = input_train[[]].copy()
res['real'] = y
res['proba'] = proba
evaluate_pr(res)

多分类

precision_recall_fscore_support: 计算每个分类的precision, recall, fscore和support

回归问题

在sklearn中, 通常函数以_score结尾返回一个值来最大化, 越高越好; 函数 _error或_loss结尾返回一个值来 minimize（最小化）, 越低越好.

平均绝对误差（MAE）

平均绝对误差MAE（Mean Absolute Error）又被称为l1
平均绝对误差是非负值，模型越好MAE越接近零.
公式 $$MAE = \frac{1}{m}\sum_{i=0}^m|y_i - \hat{y}_i|$$

sklearn相应包

sklearn.metrics.mean_absolute_error

from sklearn.metrics import mean_absolute_error

y_true, y_pred = [3, -0.5, 2, 7], [2.5, 0.0, 2, 8]
mean_absolute_error(y_true, y_pred)
# 0.5

平均平方误差（MSE）

平均平方误差MSE（Mean Squared Error）又被称为l2
本质是在残差平方和(RSS)的基础上除以了样本总量，得到了每个样本量上的平均误差.
均方误差是非负值，模型越好MSE越接近零.
公式 $$MSE = \frac{1}{m}\sum_{i=0}^m(y_i - \hat{y}_i)^2$$

sklearn相应包

sklearn.metrics.mean_squared_error

from sklearn.metrics import mean_squared_error

y_true, y_pred = [3, -0.5, 2, 7], [2.5, 0.0, 2, 8]
mse = mean_squared_error(y_true, y_pred)
# 0.375
rmse = np.sqrt(mse)
# 0.6123724356957945

均方根误差（RMSE）

均方根误差RMSE (Root Mean Squared Errort), 即MSE开方.
公式 $$RMSE = \sqrt{\frac{1}{m}\sum_{i=0}^m(y_i - \hat{y}_i)^2}$$

均方对数误差(MSLE)

均方对数误差MSLE (mean squared logarithmic error)
均方对数误差是非负值，模型越好MSLE越接近零.
公式 $$MSLE = \frac{1}{m}\sum_{i=1}^m(log(y_i + 1) - log(\hat{y_i + 1})^2$$

sklearn对应包

sklearn.metrics.mean_squared_log_error

中值绝对误差(MedAE)

中值绝对误差MedAE（median absolute error）
中值绝对误差是非负值，模型越好MSE越接近零.
公式 $$MedAE = median(|y_i - \hat{y}_i|, \cdots, |y_m - \hat{y}_m|)$$

sklearn对应包

sklearn.metrics.mean_squared_log_error

可释方差得分 (EVS)

解释变异（ Explained variance）是根据误差的方差计算得到.
最佳模型的可释方差分数值为1，模型越差值越小.
公式: $$EVS = 1 - \frac{var(y_i - \hat{y_i})}{var(y_i)}$$

sklearn相关包

sklearn.metrics.explained_variance_score

决定系数(Coefficient of Determination)

R2 决定系数(r2_score) 判断回归方程的拟合程度.
最佳模型的R^{2}决定系数分数值为1，常数模型值为0，模型越差值越小.
公式 $$ R^2 = 1 - \frac{\sum_{i=0}^m(y_i - \hat{y}i)^2}{\sum{i=0}^m(y_i - \bar{y}i)^2} = 1 - \frac{RSS}{\sum{i=0}^m(y_i - \bar{y}_i)^2} $$

sklearn相关包

sklearn.metrics.r2_score

from sklearn.metrics import r2_score
y_true, y_pred = [3, -0.5, 2, 7], [2.5, 0.0, 2, 8]
r2_score(y_true, y_pred)

聚类问题

聚类结果, 追求"簇内相似度"(intra-cluster similarity)高, 且"簇间相似度"(inter-cluster similarity)低.
聚类性能度量大致有两类:
- 将聚类结果与某个"参考模型"(reference model)进行比较, 称为"外部指标"(external index).
- 直接参考聚类结果而不利用任何参考模型, 称为"内部指标"(internal index).

外部指标

对数据集$D = {x_1, x_2, \cdots, x_m}$, 假定通过聚类给出的簇划分为$C = {C_1, C_2, \cdots, C_k }$, 参考模型给出的簇划分为$ $C^* = \{C_1^*, C_2^*, \cdots, C_s^*\}$ $. 相应地, 令$\lambda$与$ $\lambda^*$ $分别表示与$C$和$ $C^*$ $对应的簇标记向量, 将样本两两配对考虑, 定义

$$
  a = |SS|, SS = \{(x_i,x_j) | \lambda_i = \lambda_j, \lambda_i^* = \lambda_j*, i < j \} \\
  b = |SD|, SD = \{(x_i,x_j) | \lambda_i = \lambda_j, \lambda_i* \ne \lambda_j^*, i < j \} \\
  c = |DS|, DS = \{(x_i,x_j) | \lambda_i \ne \lambda_j, \lambda_i^* = \lambda_j^*, i < j \} \\
  d = |DD|, DD = \{(x_i,x_j) | \lambda_i \ne \lambda_j, \lambda_i^* \ne \lambda_j^*, i < j \}
  $$

其中
- 集合SS: 包含了在$C$中属于相同簇, 同时在$C^*$中也属于相同簇的样本对
- 集合SD: 包含了在$C$中属于相同簇, 同时在$C^*$中属于不同簇的样本对
- 集合DS: 包含了在$C$中属于不同簇, 同时在$C^*$中属于相同簇的样本对
- 集合DD: 包含了在$C$中属于不同簇, 同时在$C^*$中属于不同簇的样本对
由于每个样本对$(x_i, x_j) (i < j)$仅能出现在一个集合中, 因此有$a + b + c + d = m(m - 1)/2$

常用外部指标

Jacccard系数(Jaccard Coeffient, 简称JC) $$JC = \frac{a}{a + b + c}$$
FM指数(Fowlkes and Mallows Index, 简称FMI) $$FMI = \sqrt{\frac{a}{a + b} \cdot \frac{a}{a + c}}$$
Rand指数(Rand Index, 简称RI) $$RI = \frac{2(a + d)}{m(m-1)}$$
上述性能指数的结果值均在$[0, 1]$区间, 值越大越好.

互信息（Mutual Information)

两个随机变量的互信息（Mutual Information，简称MI）或转移信息（transinformation）是变量间相互依赖性的量度.

sklearn相应包

FMI: fowlkes_mallows_score
RI: sklearn.metrics.adjusted_rand_score
MI: sklearn.metrics.adjusted_mutual_info_score

内部指标

考虑聚类结果的簇划分$C = {C_1, C_2, \cdots, C_k}$, 有以下定义
- $avg(C)$为簇$C$内样本间的平均距离
- $diam(C)$对应簇内样本间的最远距离
- $d_{min}(C_i, C_j)$对应于簇$C_i$与簇$C_j$最近样本间的距离
- $d_{cen(C_i, C_j)}$对应簇$C_i$与簇$C_j$中心点的距离

常用内部指标

DB指数(Davies-Bouldin Index, 简称DBI) $$DBI = \frac{1}{k}\sum_{i=1}^k\max_{ j\ne i}(\frac{avg(C_i) + avg(C_j)}{d_{cen}(C_i, C_j)})$$ DBI的可能最小值为0, 值越小越好.
Dunn指数(Dunn Index, 简称DI) $$DI = \min_{1 \le i \le k}{\min_{j \ne i}(\frac{d_{min}(C_i,C_j)}{\max_{1 \le l \le k} diam(C_l)})}$$ DI值越大越好

轮廓系数（Silhouette coefficient）

结合了聚类的凝聚度（Cohesion）和分离度（Separation）, 用于评估聚类的效果。该值处于(-1,1)之间.
其中值越接近1表示样本与自己所在的簇中的样本很相似，并且与其他簇中的样本不相似;当样本点与簇外的样本更相似的时候，轮廓系数就为负; 当轮廓系数为0时, 则代表两个簇中的样本相似度一致，两个簇本应该是一个簇.
公式 $$s(i) = \frac{b(i) - a(i)}{max{a(i) , b(i)}}$$ a(i)为样本i与簇内其它样本的平均距离, b(i)为样本i与其它某簇样本的平均距离, 多个簇b(i)取最小.

sklearn相应包

DBI: sklearn.metrics.davies_bouldin_score
sklearn.metrics.silhouette_score, 返回是一个数据集中, 所有样本的轮廓系数均值.
sklearn.metrics.silhouette_score_samples，它的参数与轮廓系数一致，但返回的是数据集中每个样本自己的轮廓系数.

关联问题

假设$I={I_{1},I_{2},\ldots ,I_{m}}$, 是项的集合。给定一个交易数据库$D={t_{1},t_{2},\ldots ,t_{n}}$，其中每个事务（Transaction）t是I的非空子集，即$t\subseteq I$，每一个交易都与一个唯一的标识符TID（Transaction ID）对应。关联规则是形如$X \Rightarrow Y$的蕴涵式，其中$X,Y\subseteq I$且$X\cap Y=\emptyset$ ， X和Y分别称为关联规则的先导(antecedent或left-hand-side, LHS)和后继(consequent或right-hand-side, RHS) 。关联规则$X\Rightarrow Y$在D中的支持度（support）是D中事务包含$X\cup Y$的百分比，即概率$P(X\cup Y)$；包含X的事务中同时包含Y的百分比，即条件概率$P\left(Y|X\right)$。

支持度(Support)

表示项目X, Y同时在总数据集中出现的概率, 其计算公式为 $$support(X => Y) = \frac{T(X \cup Y)}{N}$$ 指D中N个交易记录中同时出现X和Y的交易记录所占的比例.

置信度(Confidence)

指在先导项X已经发生的情况下, 后续项Y也发生的概率, 即包含X的交易记录中同时也包含Y的交易记录所占的比例, 计算公式为: $$confidence(X => Y) = \frac{support(X \cup Y)}{support(X)}$$

提升度

表示含有X的条件下同时含有Y的概率, 与无论含不含X, 含有Y的概率之比, 计算公式 $$confidence(X => Y) /support(Y)$$ 购买X的情况下, 购买Y的概率大于购买Y的概率, 则具有提升作用.

分类问题

混淆矩阵（Confusion Matrix）

sklearn相应的包

准确率(Accuracy)

sklearn相应的包

精确率(Precision): 预测正确的正样本占所有预测为正样本的比例

sklearn相应的包

召回率 (Recall): 预测正确的正样本占所有正样本比例

sklearn

F1 score

sklearn相应的包

增益（Gain）和提升（Lift）图

ROC曲线

sklearn相应的包

AUC（Area Under Curve）

sklearn相应的包

PR曲线

曲线绘制

多分类

回归问题

平均绝对误差（MAE）

sklearn相应包

平均平方误差（MSE）

sklearn相应包

均方根误差（RMSE）

均方对数误差(MSLE)

sklearn对应包

中值绝对误差(MedAE)

sklearn对应包

可释方差得分 (EVS)

sklearn相关包

决定系数(Coefficient of Determination)

sklearn相关包

聚类问题

外部指标

常用外部指标

互信息（Mutual Information)

sklearn相应包

内部指标

常用内部指标

轮廓系数（Silhouette coefficient）

sklearn相应包

关联问题

支持度(Support)

置信度(Confidence)

提升度

参考